“Turning out the mask”

Contribution technique

This technique can help to reduce long computations with lot of variables. This kind of problems are usually of couting and combinatorics.

Problem: You will receive \(n\) points on the plane. Find how many non-degenerate triangles you can build with these points as vertices.

\[1 \leq n \leq 2000\]

First, we note that we can implement a \(O(n^3)\) solution, but we need something better. Then, we remember that if we have three no collinear points, we have a triangule. Moreover, two different points form a line. Using these ideas, we can fix a point and a line that pass throught it. If we fix the point ‘A’ of a triangle, the second vertex ‘B’ can be any other point that pass thought this line. If \(x\) points pass on this line, then \(n - x\) points are outside, so ‘C’ has \(n - x\) options. So, if we fix a point and a line that pass though it we know that this line adds \((x - 1) \cdot (n -x)\) to the answer. Then, we can use brute force over it. Nevertheless, we are doing double couting (each point is counted 3 times and in two directions). So, the answer is divided by 6.

Moreover, we would like, for example, to work with the vectors \(\{ (a, b), (2 \cdot a, 2 \cdot b), (-a, -b), \dots \}\) as if they were an unique vector. For this reason we can use its direction vector, but we need to work with integers. Check the implementation for more details.

Using these ideas we can implement a \(O(n^2 \log n)\) solution.

#include <bits/stdc++.h>

map<pair<int, int>, int> tri[maxN];

int main() {
  cin >> n;
  for (int i = 1; i <= n; ++i) {
    cin >> x[i] >> y[i];
  }
  for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= n; ++j) {
      if (i == j) {
        continue;
      }
      int vx = x[i] - x[j];
      int vy = y[i] - y[j];
      int g = __gcd(abs(vx), abs(vy));
      vx /= g;
      vy /= g;
      if (vx < 0 or vx == 0 and vy < 0) {
        vx = -vx;
        vy = -vy;
      }
      tri[i][{vx, vy}] += 1;
    }
  }
  long long ans = 0;
  for (int i = 1; i <= n; ++i) {
    for (auto v: tri[i]) {
      ans += (n - 1 - v.second) * v.second; 
    }
  }
  cout << ans / 6 << endl;
  return 0;
}
Seaching over all the permutations

There are problems where you need to search over all the permutations of \([1, 2, \dots, n]\) in order to find a solution. You can do it using the STL. For example:

#include <bits/stdc++.h>

using namespace std;

int main () {
  int n = 4;
  vector <int> arr(n);
  iota(begin(arr), end(arr), 1);
  // the array must be sorted or you won't get all the permutations
  do {
    for (int arr_i: arr) {
      cout << arr_i << ' ';
    }
    cout << '\n';
  } while (next_permutation(begin(arr), end(arr)));
  return (0);
}

The above code has complexity \(O(n! n)\).

Now, let’s see this technique in this problem.

Solution:

Note that \(abcdefghij\) can be mapped to \(0123456789\). Then, we can search the answer in \(O(\Sigma! n)\) where \(\Sigma = 10\). But \(1 \leq n \leq 1000\), so this approach would be a \(TLE\) veredict. Nevertheless, we can use a counter of frecuencies for each digit and then get the total sum using it. In this way we have an \(O(\Sigma! LS)\) solution, where \(S = 10 \land L \leq 6\). Here \(L\) is the maximum number of digits.

#include <bits/stdc++.h>

using namespace std;

const int LEN = 6, SIGMA = 10;

int cnt[LEN + 1][SIGMA + 1], val[SIGMA + 1];
bool invalid[SIGMA + 1];

int main () {
  int n;
  cin >> n;
  for (int i = 0; i < n; i++) {
    string number;
    cin >> number;
    invalid[number[0] - 'a'] = true;
    int sz = number.size();
    for (int j = 0; j < sz; j++) {
      cnt[LEN - sz + j][number[j] - 'a']++;
    }
  }
  string sigma = "abcdefghij";
  int ans = INT_MAX;
  do {
    if (invalid[sigma[0] - 'a']) continue;
    int p = 0;
    for (const char ch: sigma) val[ch - 'a'] = p++;
    int sum = 0, carry = 0, power = 1;
    for (int i = LEN - 1; i >= 0; i--) {
      int ac = 0;
      for (int j = 0; j < SIGMA; j++) {
        ac += cnt[i][j] * val[j];
      }
      ac += carry;
      sum = sum + power * (ac % 10);
      power *= 10;
      carry = ac / 10;
    }
    while (carry) {
      sum = sum + power * (carry % 10);
      power *= 10;
      carry /= 10;
    }
    ans = min(ans, sum);
  } while (next_permutation(begin(sigma), end(sigma)));
  cout << ans << endl;
  return (0);
}
Binary representation

In computer, numbers are represented as bit strings and remember that the bit representation of a number has this form:

\(X = \overline{b_kb_{k - 1} \dots b_0}_{(2)} = b_k \cdot 2^k + b_{k - 1} \cdot 2^{k - 1} + \dots + b_0 \cdot 2^0\)

In C++, the int and long long type uses 32 and 64 bits, respectively.

For example, the number 42 is

\(42 = \overline{00000000000000000000000000101010}_{(2)}\)

The leftmost bit, the most significant bit, is the sign of the number. It is 0 for nonnegative numbers and 1 for negative number. The remaining 31 or 63 bits are used for the magnitude of the number. For this reason we have:

  • int can store numbers in \([-2^{31}, 2^{31})\)
  • long long can store numbers in \([-2^{63}, 2^{63})\)

This number are store using what is called two’s complement. This technique alose allows us to represent negative numbers using this formula:

\[x < 0: value(x) = inv(-x - 1) = inv(-x) + 1\]

For example, to find the representation of -42 first invert all the bits.

\(inv(42) = \overline{11111111111111111111111111010101}_{(2)}\)

Then, increase it by one and we have:

\(-42 = \overline{11111111111111111111111111010110}_{(2)}\)

Moreover, unsigned types uses all the bits to store the value of a number, then we have:

  • unsigned int can store numbers in \([0, 2^{32})\)
  • unsigned long long can store numbers in \([0, 2^{64})\)

You may also be interested in looking at what happend with Python’s integers. Check this Link.

Bitwise operations

First, we need to recall these operators:

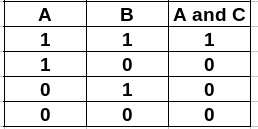
  • AND (in C++ is & or bitand)

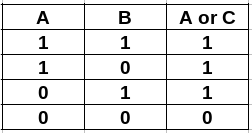
  • OR (in C++ is | OR bitor)

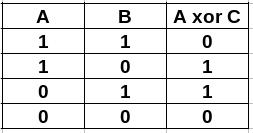
  • XOR (in C++ is ^)

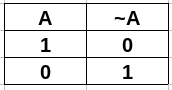
  • NOT (in C++ is ~)

In C++ we can see a number as a mask of bits, then when applying any of these operators to a number, it is applied to every bit. For example:

int a = 7;      // 00000000000000000000000000000111
int b = 33;     // 00000000000000000000000000100001
int r1 = a & b; // 00000000000000000000000000000001
int r2 = a | b; // 00000000000000000000000000100111
int r3 = a ^ b; // 00000000000000000000000000100110
int r3 = ~a;    // 11111111111111111111111111111000
int r4 = ~b;    // 11111111111111111111111111011110

And, we can even shift the bits to the left or to the right using these operators:

  • Left shift (in C++ is <<)
    • a << k moves the bits of the mask of bits of a k positions to the left and insert 0s to the right
  • Left shift (in C++ is >>)
    • a >> k moves the bits of the mask of bits of a k positions to the right and insert 0s to the left

For example:

int b = 33;      // 00000000000000000000000000100001
int x1 = b << 0; // 00000000000000000000000000100001
int x2 = b << 1; // 00000000000000000000000001000010
int x3 = b << 2; // 00000000000000000000000010000100
int x4 = b << 3; // 00000000000000000000000100001000
int y1 = b >> 0; // 00000000000000000000000000100001
int y1 = b >> 1; // 00000000000000000000000000010000
int y1 = b >> 2; // 00000000000000000000000000001000
int y1 = b >> 3; // 00000000000000000000000000000100

Moreover, you may notice that:

  • \(b << k = b \cdot 2^k\)
  • \(b >> k = b / 2^k\)

Then, particularly, we have that \(1 << k = 2^k\) and we can combine all these operator to manipulate bits. For example:

  • Get the \(k\)-th bit of \(a\):
int b_k = (a >> k) & 1;
  • Turn on the \(k\)-th bit of \(a\):
int k_on_a = a | (1 << k);
  • Turn off the \(k\)-th bit of \(a\):
int k_off_a = a & (~(1 << k));
  • Toggle the \(k\)-th bit of \(a\):
int k_toggle_a = a ^ (1 << k);

Moreover, there are some useful built functions of GCC that we can use in competitive programming, for example:

int x = 12;
int r1 = __builtin_popcount(x);
// 2 - the number of 1s in the number
int r2 = __builtin_clz(x);
// 28 - the number of zeros at the beginning
int r3 = __builtin_ctz(x);
// 2 - the number of zeros at the end

You may be interested in checking the full list of builtin funcionts of GCC.

Brute force on bitmasks

There are some kind of problem where you have \(n\) items and each item can be taken or not. Then, you can represent the states of the problems as \(S = \{ b_1b_2b_3 \dots b_n: b_i = 0 \lor b_i = 1\}\). That is, if \(b_i = 0\) we are not taken the \(i-th\) element, else we are taking it. And we can use bitmasks to simulate \(S\).

Let’s see how to use it in this problem.

If you select the same cell two times, the field is not changed. Then, we only care if each element is taken or not. Then we can simulate all the options in \(O(n^2 2^n)\) where \(n=16\) for this problem.

#include <bits/stdc++.h>

using namespace std;

int main () {
  int dr[] = {0, 1, 0, -1, 0};
  int dc[] = {0, 0, 1, 0, -1};
  vector <string> grid(4);
  vector <string> black(4, string(4, 'b'));
  vector <string> white(4, string(4, 'w'));
  for (int i = 0; i < 4; i++) cin >> grid[i];
  int ans = INT_MAX;
  for (int mask = 0; mask < (1 << 16); mask++) {
    vector <string> tmp = grid;
    int cnt = 0;
    for (int bit = 0; bit < 16; bit++) {
      if ((mask >> bit) & 1) {
        cnt++;
        int r = bit / 4;
        int c = bit % 4;
        for (int d = 0; d < 5; d++) {
          int nr = r + dr[d];
          int nc = c + dc[d];
          if (0 <= min(nr, nc) and max(nr, nc) < 4) {
            if (tmp[nr][nc] == 'b') tmp[nr][nc] = 'w';
            else tmp[nr][nc] = 'b';
          }
        }
      }
    }
    if (tmp == black or tmp == white) {
      ans = min(ans, cnt);
    }
  }
  if (ans == INT_MAX) puts("Impossible");
  else cout << ans << endl;
  return (0);
}

Recommended readings:

Contest

You can find the contest here.

Nice Garland

If we fix the first three elements, we can know how all the sequence should be. Then we can try to find the answer in all the permutations of the string “RGB”.

#include <bits/stdc++.h>

using namespace std;

int main () {
  ios::sync_with_stdio(false);
  cin.tie(0);
  int n;
  cin >> n;
  string s;
  cin >> s;
  vector <char> p = {0, 1, 2};
  string X = "RGB";
  int mn = INT_MAX;
  string ans;
  do {
    int cnt = 0;
    for (int i = 0; i < 3 and i < s.size(); i++) {
      for (int j = i; j < s.size(); j += 3) {
        cnt += s[j] != X[p[i]];
      }
    }
    if (cnt < mn) {
      mn = cnt;
      string ret = "";
      for (int k = 0; k < s.size(); k++) {
        ret += X[p[k % 3]];
      }
      ans = ret;
    }
  } while (next_permutation(begin(p), end(p)));
  cout << mn << endl;
  cout << ans << endl;
  return (0);
}

Petr and a Combination Lock

Each angle can be used to rotate in a clockwise or counterclockwise direction (i.e each angle have two options), then we can use a mask with \(n\) bits to simulate all possible states.

#include <bits/stdc++.h>

using namespace std;

int n;
vector <int> angle;

bool check (int mask) {
  int cur = 0;
  for (int bit = 0; bit < n; bit++) {
    if ((mask >> bit) bitand 1) cur += angle[bit];
    else cur -= angle[bit];
  }
  return (cur % 360) == 0;
}

int main () {
  cin >> n;
  angle.resize(n);
  for (int i = 0; i < n; i++) cin >> angle[i];
  bool ok = false;
  for (int mask = 0; mask < (1 << n); mask++) ok |= check(mask);
  puts(ok ? "YES" : "NO");
  return (0);
}

Splitting Numbers

Just simulate what the problem says.

#include <bits/stdc++.h>

using namespace std;

int main () {
  int num;
  while (cin >> num, num != 0) {
    int num1 = 0;
    int num2 = 0;
    int cnt = 0;
    for (int bit = 0; bit < 32; bit++) {
      if (not ((num >> bit) & 1)) continue;
      if (cnt & 1) num2 |= (1 << bit);
      else num1 |= (1 << bit);
      cnt++;
    }
    cout << num1 << ' ' << num2 << '\n';
  }
  return (0);
}

Number of Parallelograms

We can say that \(\square ABCD\) is a parallelogram if and only if \(\overrightarrow{AB} = \overrightarrow{CD}\). Then, you can store all the possible vectors that you can form with these points, now if there are \(x\) vectors \(\overrightarrow{AB}\), you can form \(\binom{x}{2} / 4\) parallelograms.

#include <bits/stdc++.h>

#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair

using namespace std;

typedef long long ll;
typedef pair <int, int> pii;

int main () {
  ios::sync_with_stdio(false); cin.tie(0);
  int n;
  cin >> n;
  map <pii, int> mp;
  vector <pii> p (n);
  for (int i = 0; i < n; i++) cin >> p[i].first >> p[i].second;
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      if (i == j) continue;
      pii v;
      v.first = p[i].first - p[j].first;
      v.second = p[i].second - p[j].second;
      mp[v]++;
    }
  }
  ll ans = 0;
  for (auto pp: mp) ans += 1LL * pp.second * (pp.second - 1) / 2;
  cout << ans / 4 << '\n';
  return (0);
}

Next

Previous