“Try every possibility”

Problem solving paradigms

A programming paradigm is a way to solve problems. The four problem solving paradigms commonly used in programming contests are:

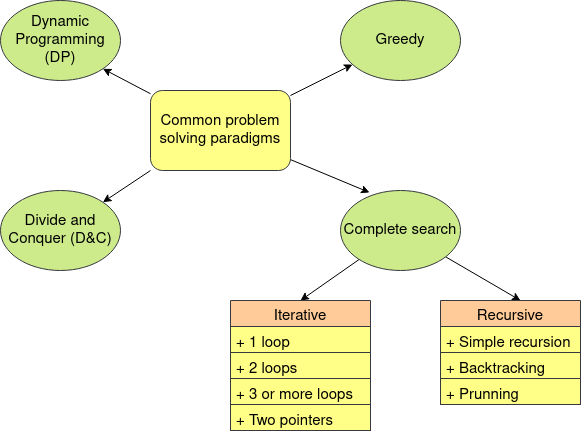
Complete search is a general method that can be used to solve almost any algorithm problem. It basically try to generate all possible solutions of a problem in order to do something with them (count number of elements, find a particular solution with one property, etc).

You can find complete search solutions in two ways: iterative and recursive. When it is iterative it may be a single loop, two loops, three or more loops, using two pointers, etc. When it is recursive it can be a simple recursive function, it can be a recursive function that search different states with trial and error (backtracking), it may have some kind of prunning in order to not visit every state, etc.

When solving complete search solutions you will follow some combination of these structures to solve problems.

When you find complete search in a iterative way it is called a brute force solution. In the next 4 classes we will study more about this kind of solutions. Moreover, mastering this paradigm will help you to understand easily the other ones.

Pythagorean triples

Let’s start this paradigm solving a simple problem.

A pythagorean triple is a triplet (x,y,z) that satisfies the equation \(x^2 + y^2 = z^2\).

Problem: You will receive an integer \(n\). Find the number of pythagorean triples such that \(1 \leq x, y, z \leq n\).

\[1 \leq n \leq 10^3\]

First solution

We can fix \(x, y, z\) using three loops and verify if the equation holds in \(O(n^3)\).

int solution1 (int n) {
  int cnt = 0;
  for (int x = 1; x <= n; x++) {
    for (int y = 1; y <= n; y++) {
      for (int z = 1; z <= n; z++) {
        if (x * x + y * y == z * z) {
          cnt++;
        }
      }
    }
  }
  return cnt;
}

We can fix \(x, y\) and determine if \(\exists \, 1 \leq z \leq n\) that holds the equation in \(O(n^2)\).

Second solution

int solution2 (int n) {
  vector <bool> is_sq(n * n + 1, false);
  for (int z = 1; z <= n; z++) {
    is_sq[z * z] = true;
  }
  int cnt = 0;
  for (int x = 1; x <= n; x++) {
    for (int y = 1; y <= n; y++) {
      if (x * x + y * y <= n * n and is_sq[x * x + y * y]) {
        cnt++;
      }
    }
  }
  return cnt;
}

Third solution

If \((x, y, z)\) is a pythagorean triple, then \((kx, ky, kz), k \in \mathbb{N}\) is also a pythagorean triple.

So, if we find \((x, y, z) \mid gcd(x, y, z) = 1\), then the number of triples \((kx, ky, kz) : 1 \leq kx, ky, kz \leq n\) is \(\min(\lfloor n / x \rfloor, \lfloor n / y \rfloor, \lfloor n / z \rfloor )\).

If \((x, y, z)\) is a pythagorean triple and \(gcd(x, y, z) = 1\), then \((x, y, z)\) is called a primite pythagorean triple.

And there is a property (Euclid’s formula) that says that every primite pythagorean triple can be represented by a pair \((a, b) \mid 0 < b < a \land gcd(a, b) = 1 \land a\) and \(b\) are not both odds in the following way:

\[x = a^2 - b^2\] \[y = 2 \cdot a \cdot b\] \[z = a \cdot a + b \cdot b\]

(Notice that we can build a right triangle with \(x, y, z\)).

Moreover, we have: \[a \cdot a \leq a \cdot a + b \cdot b \leq z \leq n\]

Then, a can just take values in \([0, \sqrt{n}]\). So we can generate primites \((x, y, z) \land (y, x, z)\) and count how many of their multiples hold the condition of the problem in \(O((\sqrt{n}) \cdot \sqrt{n} \cdot \log n) = O(n \log n)\).

Note:

\(gcd(a, b) =\) greatest common divisor of \(a\) and \(b = \max(d: d | a \land d | b \land d > 0)\)

int solution3 (int n) {
  int cnt = 0;
  for (int a = 1; a * a < n; a++) {
    for (int b = 1; b < a; b++) {
      if (__gcd(a, b) != 1) continue;
      if (a % 2 and b % 2) continue;
      int x = a * a - b * b;
      int y = 2 * a * b;
      int z = a * a + b * b;
      int add = min({n / x, n / y, n / z});
      cnt += 2 * add;
    }
  }
  return cnt;
}

Full code

Primality Test

Problem: Given a number \(n\), determine if it is prime or not,

Definition: A prime number is a natural number that have exactly two divisors. The first prime numbers are \(2, 3, 5, 7, 11, 13, \dots\)

First solution

We can use the given definition and implement a \(O(n)\) solution.

bool isPrime1 (int n) {
  int n_div = 0;
  for (int d = 1; d <= n; d++) {
    if (n % d == 0) n_div++;
  }
  return (n_div == 2);
}

Second solution

We notice that if \(d | n \to \frac{n}{d} | n\). Moreover: \[\text{If } d \not = \sqrt{n} \to (d < \sqrt{n} < \frac{n}{d}) \lor (\frac{n}{d} < \sqrt{n} < d)\]

So we can assume \(d < \frac{n}{d}\) iterate for every \(d < \sqrt{n}\) and if \(d | n\) count two more divisors (\(d, \frac{n}{d}\)) and handle the special case \(d = \sqrt{n}\). In this way we can count the number of divisors of \(n\) and check if a number is prime in \(O(\sqrt{n})\).

bool isPrime2 (int n) {
  int n_div = 0;
  for (int d = 1; d * d <= n; d++) {
    if (n % d == 0) {
      n_div++;
      if (n / d != d) n_div++;
    }
  }
  return (n_div == 2);
}

Full code

Sieve of Eratosthenes

We want to solve the same problem of the previous section but now we want to be able to handle multiples queries in an optimal way. Then, we want to store an array where we can get whether or not a number is prime.

We can use a simple idea to achieve that. We will initiate with an array where every element is true (it will represent that the number is prime). Then we will iterate from \(2\) to \(n\) and every time we find a prime number, we set to false its multiples that are greater than it.

As every prime number have only two divisors (1 and itself), and we are iterating from the number 2, then when we are in the number \(i\) in the iteration if \(i\) is a prime number it will be set to true, else \(\exists \, p\) (prime) \(: p < i \land p | i\), so the array will already be set to false in that position.

We can use this idea and implement an algorithm to obtain such array. The special cases (i.e \(n = 0 \lor n = 1\)) can be handle easily. The complexity of this solution is \(O(n \log \log n)\).

vector <bool> sieve (int n) {
  vector <bool> is_prime(n + 1, true);
  is_prime[0] = is_prime[1] = false;
  for (int i = 2; i <= n; i++) {
    if (!is_prime[i]) continue;
    for (int j = 2 * i; j <= n; j += i) {
      is_prime[j] = false;
    }
  }
  return is_prime;
}

Full code

Finding the number of divisors of a number

Note: \[\sigma_{0}(n) = \text{ number of divisors of } n\]

We have already written a program that computes the number of divisors in \(O(n)\) and in \(O(\sqrt{n})\). But, we can use an idea similar to the one we used in the previous section to get \(\sigma_{0}(x), 1 \leq x \leq n\) efficiently.

vector <int> nDivisors (int n) {
  vector <int> n_div(n + 1, 0);
  for (int i = 1; i <= n; i++) {
    for (int j = i; j <= n; j += i) {
      n_div[j] += 1;
    }
  }
  return n_div;
}

Full code

The complexity of the above algorithm is:

\[n + \frac{n}{2} + \frac{n}{3} + \frac{n}{4} + \dots + \frac{n}{n}\] \[n \cdot (1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots + \frac{1}{n})\] \[n \cdot H_{n} < n \log n\]

So, the complexity of our program is \(O (n \log n)\).

\(\sigma_{0}(n) = O(\sqrt[3]{n})\)

There are some problems that looks like a brute force solution would give a Time Limit veredict. One common example of this kind of problem are the ones where you need to do something with the divisors of a number. You will face one problem of this kind in one of your contests.

Recommended readings:

Contest

You can find the contest here.

Simple Equations

\[0 \leq x^2 \quad \forall x \in \mathbb{N}\] \[\to x^2 \leq x^2 + y^2 + z^2 = C\] \[x^2 \leq C\] \[|x| \leq \sqrt{C}\] \[-\sqrt{C} \leq x \leq \sqrt{C}\] The same hold for \(x, y, z\). Moreover if we have fixed \(x, y\), then \(z = A - x - y\). So, we can fix \(x, y\) in \(O(\sqrt{C}^2) = O(C)\) and verify if \(x, y, z\) holds the equations in \(O(1)\). Don’t forget \(x, y, z\) must be different.

#include <bits/stdc++.h>

using namespace std;

void solve (int A, int B, int C) {
  int lim = sqrt(C) + 1;
  for (int x = -lim; x <= lim; x++) {
    for (int y = -lim; y <= lim; y++) {
      int z = A - x - y;
      if (x == y or x == z or y == z) continue;
      if ((x + y + z == A) and
          (x * y * z == B) and
          (x * x + y * y + z * z == C)) {
        cout << x << ' ' << y << ' ' << z << '\n';
        return;
      }
    }
  }
  cout << "No solution.\n";
}

int main () {
  int tc;
  cin >> tc;
  while (tc--) {
    int A, B, C;
    cin >> A >> B >> C;
    solve(A, B, C);
  }
  return (0);
}

Common Divisors

\(S = \{x: x | a_i \quad \forall i \in [1, n] \}\)

Let \(g = \gcd(a_1, a_2, \dots, a_n)\).

Affirmation: \(S = \{x: x | g \}\). (The proof is left to the reader)

Then, we just need to find \(\sigma_0(g)\) and we can do it in \(O(\sqrt{n}))\).

#include <bits/stdc++.h>

#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())

using namespace std;

typedef long long ll;
typedef pair <int, int> pii;

int main () {
  ios::sync_with_stdio(false); cin.tie(0);
  int n;
  cin >> n;
  vector <ll> arr(n);
  cin >> arr[0];
  ll g = arr[0];
  for (int i = 1; i < n; i++) cin >> arr[i], g = __gcd(g, arr[i]);
  ll ans = 0;
  for (ll d = 1; d * d <= g; d++) {
    if (g % d) continue;
    ans++;
    ll d2 = g / d;
    if (d == d2) continue;
    ans++;
  }
  cout << ans << '\n';
  return (0);
}

2Char

The key of the problem is to notice what the search space is. As every valid text would have at most two characters and maximum length, then we can fix what would be the two characters and take all the strings that just have these characters.

#include <bits/stdc++.h>

using namespace std;

const int MAX_N = 110;

int n, ans;
string word[MAX_N];

bool isValid(int id, char ch_1, char ch_2) {
  for (int pos = 0; pos < word[id].size(); pos++) {
    if (word[id][pos] != ch_1 and word[id][pos] != ch_2) {
      return false;
    }
  }
  return true;
}

int main() {
  cin >> n;
  for (int i = 0; i < n; i++) cin >> word[i];
  for (char ch_1 = 'a'; ch_1 <= 'z'; ch_1++) {
    for (char ch_2 = ch_1; ch_2 <= 'z'; ch_2++) {
      int sum = 0;
      for (int id = 0; id < n; id++) {
        sum += isValid(id, ch_1, ch_2) * word[id].size();
      }
      ans = max(ans, sum);
    }
  }
  cout << ans << endl;
  return (0);
}

Hyperset

If we have fixed two cards, we can compute what card do we need to make a set. Take care of your implementation.

#include <bits/stdc++.h>

#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair

using namespace std;

typedef unsigned long long ll;
typedef pair <int, int> pii;

int main () {
  ios::sync_with_stdio(false); cin.tie(0);
  int n, k;
  cin >> n >> k;
  vector <string> arr(n);
  map <string, int> mp;
  for (int i = 0; i < n; i++) {
    cin >> arr[i], mp[arr[i]]++;
  }
  ll ans = 0;
  for (int i = 0; i < n; i++) {
    for (int j = i + 1; j < n; j++) {
      string need = string(k, ' ');
      for (int t = 0; t < k; t++) {
        if (arr[i][t] == arr[j][t]) {
          need[t] = arr[i][t];
        } else {
          if ('S' != arr[i][t] and 'S' != arr[j][t]) need[t] = 'S';
          if ('E' != arr[i][t] and 'E' != arr[j][t]) need[t] = 'E';
          if ('T' != arr[i][t] and 'T' != arr[j][t]) need[t] = 'T';
        }
      }
      ans += mp[need];
    }
  }
  cout << ans / 3 << '\n';
  return (0);
}

Next

Previous