“Think big”

Let’s say we want to solve the following problem:

Given an array of size \(n\), sort the elements in the array.

We quickly come up with a solution, but we don’t know how efficient it is.

  • How long will my program take to run for \(n = 10 ^ 5\)?
  • How efficient it is to measure the performance of our code manually?
  • How can we compare our solution with other solutions?
  • How can we measure the performance of our code?
Sampling an extrapolation

A first approach for measuring the performance of our solution is to experimentally take time measurements for different input sizes and trying to analyze the trend that the time follows. An easy way of doing this is by plotting the input size against time to get a function we can then extrapolate. Using this method we can then experimentally compare the different algorithms we want to test. However, to do this we would have to implement all algorithms or it would be impossible to take times.

For example, if we would like to measure the time performance of this function:

vector <bool> sieve (int n) {
  vector <bool> is_prime(n, true);
  is_prime[0] = is_prime[1] = false;
  for (int i = 2; i < n; i++) {
    if (!is_prime[i]) continue;
    for (int j = i + i; j < n; j += i) {
      is_prime[j] = false;
    }
  }
  return is_prime;
}

We can run the program for different values of \(n\) and take times. We can even write a program like this and get this data:

n time (s)
1000000 0.099296
1100000 0.092526
1200000 0.098912
1300000 0.108183
1400000 0.118805
1500000 0.121858
1600000 0.127802
1700000 0.133683
1800000 0.142920
1900000 0.157752

Then, we can extrapolate a function from these points. Let

\[f(x) = \text{aprox. running time of sieve(x)}\]

As you can probably imagine, this is not the most efficient process, as it is very time consuming to do this kind of testing, specially in the scenario of a time based competition as it is competitive programming. This inevitably leads to the question: is there a better way to compare our solutions?

Big Oh notation

Our programs consists of a sequence of instructions. Now, let’s call a instruction as basic if is it one of the following cases:

  • It creates a variable or assigns a primite value to it
  • It does an arithmetic operation (\(+, -, *, /, %\))
  • It calls a function
  • It does bitwise operations (and, or, xor, not)

Now, let’s focus on finding a function \(g\) defined as:

\[g(x) = \text{# basic operations our program does for input } x\]

Now, consider that \(T = 10^8\) is the number of basic operations our computer can execute in a second. Then, we can say:

\[f(x) \approx \frac{g(x)}{T}\]

But, we can get \(g(x)\) just analyzing our code, then we can estimate \(f(x)\) without executing our program. Nevertheless, \(g(x)\) will usually have this form:

\[g(x) = a_n x^m + a_{m - 1} x^{m - 1} \dots a_1 x + a_0\]

It may take a lot of time to manually get \(g(x)\), but we notice that as \(x\) increases, the value of \(g(x)\) is dominated by its most significant term, then we can consider:

\[g(x) \approx x^m\]

And we say that \(g(x) \in O(x^m)\). But, for simplicity let’s write it as \(g(x) = O(x^m)\).

Examples:

  • \(g(n) = 100n^2 + 1000000n + 505 = O(n^2)\)
  • \(g(n) = n^5 + 10^{100}n^4 = O(n^5)\)
  • \(g(n) = 5n + 12 = O(n)\)
  • \(g(n) = 100.1 n ^ 2 + \pi n + 1 = O(n^2)\)
  • \(g(n) = 100 = O(1)\)

Here we are using Big Oh notation. It is the formal way to express the upper bound of the function. Usually, when solving a problem, finding the big oh of a function is as simple as simplifying it to its highest order term. However, a more formal definition of Big Oh exists:

\[f(n) = O(g(n)) \rightarrow f(n) \leq c \cdot g(n) \quad \forall n > n_0 \, \exists c > 0\]

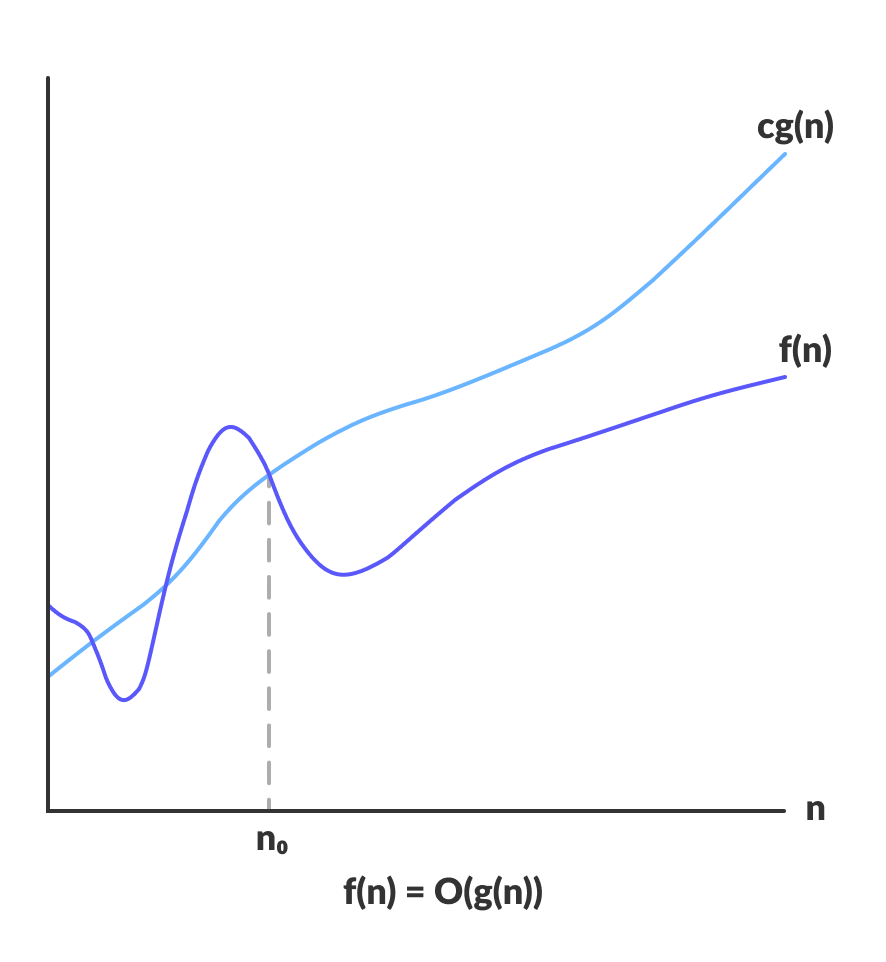
This definition says that a function \(f(n)\) is considered to have a Big Oh of \(g(n)\) if there exists a value of \(c\) such that \(c \cdot g(n)\) will be greater than \(f(n)\) from some value \(n_0\) of \(n\) onwards. From this definition it is important to note some things:

  1. Many functions \(g(n)\) can satisfy the condition \(f(n) = O(g(n))\)
  2. \(O(g(n))\) can be seen as the set of all functions that are an upper-bound to function \(f(n)\)
  3. As \(O(g(n))\) represents a set, then we should say \(f(n) \in O(g(n))\), but it is usually written as \(f(n) = O(g(n))\) for simplicity.

More examples:

  • \(g(n) = nlgn + n = O(nlgn)\)
  • \(g(n) = n! + n^2 = O(n!)\)
  • \(g(n) = 2^n + n^5 = O(2^n)\)
  • \(g(n) = n \log n + n = O(n \log n)\)
  • \(g(n) = n \sqrt{n} + n^2 = O(n^2)\)

One of the best things about estimating performance using asymptotic analysis is that it is not necessary to implement a solution in order to check if it would work or not. This way, if we have an idea for solving a problem, we can first check if our idea is fast and within the time restrictions, and then implement it, saving us the time of implementing a wrong solution just to realize that it exceeds the time limit when is sent.

Moreover, in competitive programming we usually can know the expected complexity of a valid solution according to the constrains of the problem. For example:

input size usually valid time complexity
\(n \leq 10\) \(O(n!)\)
\(n \leq 20\) \(O(2^n)\)
\(n \leq 500\) \(O(n^3)\)
\(n \leq 5000\) \(O(n^2)\)
\(n \leq 10^6\) \(O(n) \text{ or } O(n \log n)\)
\(n > 10^6\) \(O(1) \text{ or } O(\log n)\)

Source: Antti Laaksonen.Competitive programmer’s handbook - chapter 2

Asymptotic Analysis

It is a method for defining the mathematical boundaries of the run-time performance or space usage of programs as the input size increases. Useful for estimating the time and space complexity in function of the input size.

Using asymptotic analysis we can easily estimate:

  • Lower Bound - \(\Omega(f(n))\) Omega notation
  • Upper Bound - \(O(f(n))\) Big Oh notation
  • Tight Bound - \(\Theta(f(n))\) Theta notation

In this course (and usually in competitive programming) we will only explore big oh analysis, as we usually only care about the worst possible running time of our algorithm. It is better to overestimate complexity and have a extremely fast solution than to underestimate it and have a sometimes slow one.

Space and Time Complexity

When describing the performance of an algorithm, the word complexity is commonly used. Complexity can be considered as the amount of resources my algorithm will consume, and it comes in two common ways:

  • Time complexity: How long will my program take to run for a given input.
  • Space complexity: How much space will my program consume for a given input.

In many cases there exists a trade-off between space-usage and run-time performance, for this reason it is important to always check the time and space complexity of a solutions before implementing it to ensure our solutions stays within the allowed bounds.

Recommended readings:

Contest

You can find the contest here.

Problem A: Bit++

The problem is bassically to see if the input is either “X++”, “++X”, “—X” or “X—”.

The following code use this idea. But, we only look in the middle character because that is enough to verificate.

#include <bits/stdc++.h>

using namespace std;

int main () {
  int n, x = 0;
  cin >> n;
  string sta;
  while (n--) {
    cin >> sta;
      if (sta[1] == '+') x++;
      else x--;
  }
  cout << x << '\n';
  return (0);
}

Problem B: Beautiful Matrix

Here, we look for what is the difference between row position and column position of the 1 and the matrix’s center (the matrix’s center is in position 3 in axis x and y).

So, we just need to subtract in absolute value for each axis and add them.

#include <bits/stdc++.h>

using namespace std;

int main () {
  int ans;
  for (int i = 1; i < 6; i++) {
    for (int j = 1; j < 6; j++) {
      int num;
      cin >> num;
      if (num) {
        ans = abs(i - 3) + abs(j - 3);
      }
    }
  }
  cout << ans << '\n';
  return 0;
}

Problem C: Tram

In this problem, we need to keep the maximum value of passengers in each stop. With the maximum value we can ensure the minimum capacity of the tram line.

#include <bits/stdc++.h>

using namespace std;

int main () {
  int n, a, b, temp = 0, maxi = 0;
  cin >> n;
  while (n--) {
    cin >> a >> b;
    temp += b - a;
    maxi = max(maxi, temp);
  }
  cout << max << '\n';
  return 0;
}

Problem D: Elephant

For this problem, the elephant can move in steps with width of 1, 2, 3, 4 or 5. So, it is convenient to move with the maximum allowed step if we want to minimize the number of steps to the elephant meet with its friend.

Here the maximum allowed step is the step less or equal to the current distance between the elephant and its friend.

Also, we work with modular operation to calculate faster the steps.

#include <bits/stdc++.h>

using namespace std;

int main () {
  int x;
  int steps = 0;
  cin >> x;
  for (int i = 5; i > 0; i--){
    if (x >= i) {
      steps += x / i;
      x % = i;
    }
  }
  cout << steps << '\n';
  return 0;
}

Problem E: Even Odds

Firstly, the problem tells us that the sequence is all odd integers from 1 to n and then all even integers from 1 to n. 

Take care if n is even or odd. In case n is odd, we need to add one element in the odd integers block.

So, we need to calculate how many odd integers we have. Then we just check if the requested position is before or after of odd integers block.

#include <bits/stdc++.h>

using namespace std;

int main () {
  long long num, k;
  cin >> num >> k;
  long long aux = num / 2;
  if (num % 2 != 0) aux++;
  if (k > aux) {
    cout << 2 * (k - aux) << '\n';
  } else {
    cout << 2 * (k - 1) + 1 << '\n';
  }
  return 0;
}

Next

Previous